Article original : L. Poulet, J.-P. Fontaine, and C.-G. Dussap (2018) A Physical Modeling Approach for Higher Plant Growth in Reduced Gravity Environments, Astrobiology, 18:9, 1093-1100, DOI: http://doi.org/10.1089/ast.201... Proposé par : Lucie Poulet, Post-Doctorante Institution :  NASA Kennedy Space Center, Florida, USA Article relu et amendé par : la classe de Terminale de l’Institution Sévigné de Mme Dugat

*****

Résumé

Inclure des plantes dans les systèmes support-vie permet simultanément la production de nourriture et le recyclage de l’eau et de l’air. Pour comprendre et prédire le comportement des plantes pour une large gamme de paramètres environnementaux (par exemple : la température, la ventilation, la gravité), un modèle mécanistique est développé. L’accent ici est mis sur les influences respectives des niveaux de gravité (impesanteur, martienne, lunaire, terrestre) et de la convection forcée sur les échanges gazeux au niveau des feuilles (c’est-à-dire, la photosynthèse). Cette étude souligne l’importance d’étudier la couche limite, le but final étant de développer un modèle mécanistique complet de la croissance des plantes dans des environnements de gravite réduite.

Mots clés Systèmes support-vie biorégénératifs ; Modèle mécanistique ; Echanges gazeux ; gravité réduite ; Plantes ; Espace ; Écosystème artificiel ; Flux d’énergie

1. Contexte

Un systèmes support-vie (LSS1) permet d’assurer les besoins vitaux des astronautes lors des missions spatiales : apport d’air respirable, d’eau potable, de nourriture et de traitement des déchets. Pour des missions longue durée pour lesquelles l’autonomie par rapport à la Terre sera nécessaire, il faudra un LSS régénératif, capable de recycler l’air, l’eau et les déchets et de produire de la nourriture (Mitchell, 1994).

Un systèmes support-vie (LSS1) permet d’assurer les besoins vitaux des astronautes lors des missions spatiales : apport d’air respirable, d’eau potable, de nourriture et de traitement des déchets. Pour des missions longue durée pour lesquelles l’autonomie par rapport à la Terre sera nécessaire, il faudra un LSS régénératif, capable de recycler l’air, l’eau et les déchets et de produire de la nourriture (Mitchell, 1994).

La seule façon de produire de la nourriture in-situ est d’incorporer des processus biologiques dans le LSS (Wheeler, 2004) – on parle alors de LSS biorégénératifs – et alors toutes les fonctions sont interconnectées, comme c’est le cas dans la boucle MELISSA (Micro-Ecological Life-Support System Alternative2) (voir Erreur ! Source du renvoi introuvable.) développée par l’agence spatiale européenne (ESA3). C’est un écosystème artificiel base sur des bactéries, des micro-algues et des plantes. Pour que ce système soit robuste et fiable, il faut comprendre toute sa dynamique, en particulier être capable de prévoir combien notre système va pouvoir produire d’oxygène, d’eau et de biomasse en cas de panne (par exemple si l’éclairage s’arrête de fonctionner).

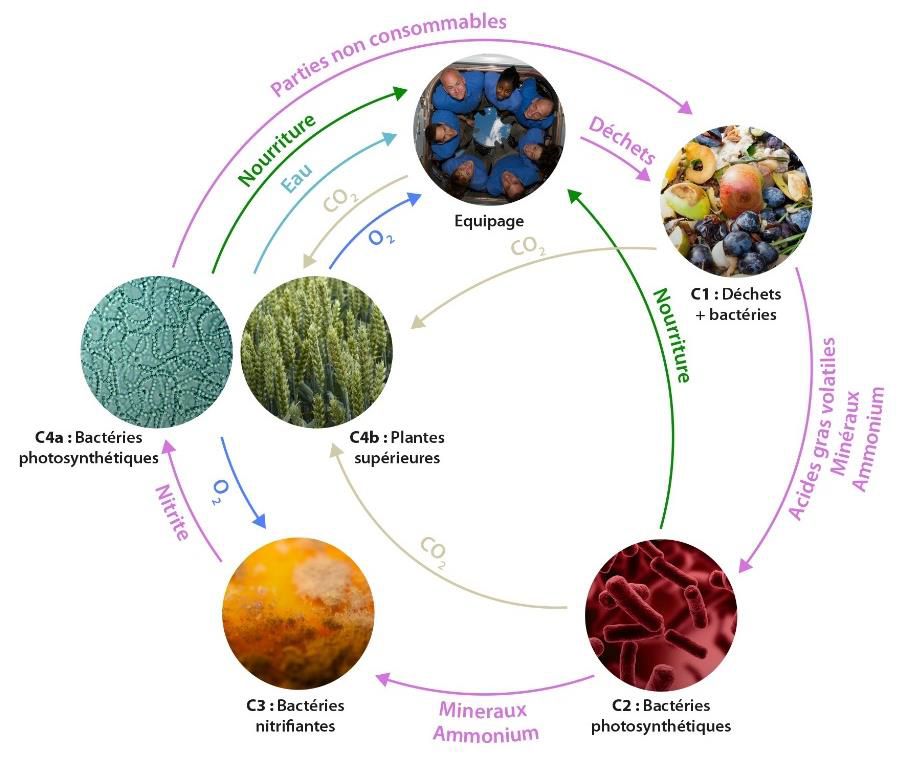
C’est pourquoi nous nous intéressons ici à l’influence des environnements de gravité réduite (l’impesanteur et les gravites martienne et lunaire) sur la croissance des plantes et comment la modéliser. Des expériences passées ont montré qu’en impesanteur, en raison de l’absence de convection naturelle4, des épaisses couches d’air stagnant se forment autour des feuilles (Kitaya, 2003), c’est la couche limite5. Lorsque cette couche limite s’épaissit, les échanges gazeux au niveau de la feuille, c’est-à-dire la photosynthèse, diminuent. Cela pourrait avoir un effet négatif sur la production de nourriture à long terme. En revanche, avec une ventilation adaptée, ces effets tendent à diminuer. Nous regardons donc les influences relatives de la convection naturelle et de la convection forcée et le lien avec l’épaisseur de couche limite, les échanges gazeux et la production de biomasse.

2. Protocole expérimental : modéliser les plantes ?? 2.1. Vous avez dit modèle ? Un modèle permet de représenter un processus de manière simplifiée et formalisée, permettant de mieux le comprendre et de l’analyser, ainsi que de prévoir des tendances pour certaines conditions. Par exemple, les prévisions météorologiques sont données par des modèles complexes ; nos courbes de croissance moyenne sont également le fruit de modèles : d’après des observations empiriques6 sur une grande partie de la population, on a pu en déduire les paliers de croissance des enfants et des normes pour chaque âge de leur vie. Il y a les variables d’entrée du modèle, qui sont les conditions de départ et il y a les variables de sortie, qui sont le résultat du modèle. Par exemple, pour une courbe de croissance les paramètres d’entrées sont l’âge et le sexe et la variable de sortie est la taille. Le domaine d’application du modèle définit les valeurs pour lesquelles le modèle est valide. En poursuivant notre exemple de courbes de croissance, le domaine d’application est (fille ; 0-1 an), (garçon ; 0-1 an), (fille ; 1-3 ans), (garçon ; 1-3 ans), etc. Si on cherche à calculer la taille d’une fille de 2 ans avec le modèle (garçon ; 1-3 ans), les résultats donnés par le modèle seront erronés. Différents types d’approches existent : 1- Développer un modèle dans le but de faire des prédictions précises pour des applications spécifiques et directes. Par exemple : prédire le rendement d’un champ de blé sur le mois de juin, avec une pluviométrie de 5 cm et une température moyenne de 20°C. Ces modèles, dits empiriques, sont développés à partir de données et observations empiriques pour un domaine d’application spécifique, sans toutefois apporter de la compréhension sur les phénomènes étudiés car ils fonctionnent comme des « boites noires ». 2- Développer un modèle pour comprendre les phénomènes et mécanismes sous-jacents, en faisant le moins d’approximations empiriques possible, on parle alors de modèles de connaissance ou de modèle mécanistiques. L’approche est multi-échelle et il s’agit de traduire en équations des phénomènes physiques, chimiques et biologiques régissant le système étudié. L’approche suivie ici est mécanistique, avec le but de comprendre les échanges gazeux des plantes en environnement de gravite réduite.

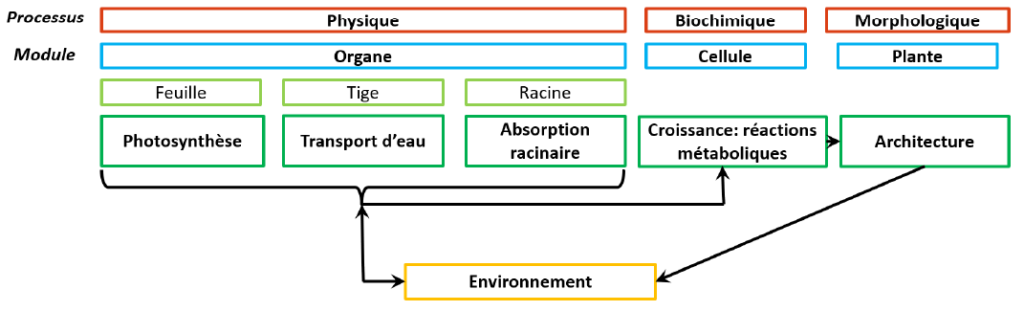
2.2. Pas n’importe quel modèle ! Le modèle ici est découpé en quatre sous-parties (Hézard, 2012), ou modules, qui correspondent aux différents niveaux d’études (voir Erreur ! Source du renvoi introuvable.) :

• Un module environnemental qui gère les variations des paramètres environnementaux,
• Un module physique, pour les effets à l’échelle de l’organe. Les quantités de carbone, de dioxygène et d’eau absorbées et rejetées par la plante, résultats des échanges gazeux, y sont calculées. Un module biochimique pour les effets au niveau cellulaire. La production de biomasse notamment dépend de l’équation chimique de la photosynthèse et est une fonction intégrale des quantités de carbone et d’eau accumulées sur une période de temps. Un module morphologique qui étudie les changements au niveau de l’échelle de la plante. En première approximation, la plante est assimilée à une seule feuille circulaire, comprenant une surface foliaire, une longueur de tige et un nombre de vaisseau dans la tige. Ces variables morphologiques varient linéairement en fonction de la biomasse produite. Grâce à des paramètres d’entrée spécifiques aux espèces, ce modèle peut être adapté à toute espèce de plante.

2.3. Comment ça, « les échanges gazeux des plantes » ? Les flux de matière expriment la quantité par seconde de carbone fixé, de lumière reçue par la plante, d’eau absorbée et produite. Tous les flux de matière maximums (𝜙𝑋) sont calculés comme étant fonction d’un coefficient de transfert (𝑘𝑋) et d’un gradient de concentrations entre l’intérieur de la feuille et l’extérieur (Δ𝐶) (Beek et al., 1999) : 𝜙𝑋= 𝑘𝑋Δ𝐶 (1) Le coefficient de transfert se calcule à partir d’un coefficient de diffusion (𝐷𝑋), propre à chaque gaz, et de l’épaisseur de couche limite (𝛿) : 𝑘𝑋= 𝐷𝑋𝛿 (2) Le plus petit des flux calculés à partir de l’équation (1) est appelé flux limitant. Par exemple, même si la plante reçoit une lumière illimitée, si le flux d’eau absorbée est limitant, c’est-à-dire si elle ne peut pas absorber assez d’eau, elle ne pourra faire de la photosynthèse au-delà de ses réserves en eau (et donc fixer du carbone et produire de la vapeur d’eau). Les autres flux sont alors recalculés en fonction du flux limitant, grâce à des relations chimiques et biochimiques découlant de la réaction métabolique de la photosynthèse.

2.4. Mais la gravité dans tout ça ? Pour prendre en compte la gravité dans les équations précédentes, il faut faire trois hypothèses :

1. L’air au-dessus de la feuille n’est pas turbulent et l’épaisseur de la couche limite peut alors s’exprimer comme une fonction de la vitesse de l’air 𝑉𝑏 : 𝛿=𝑓(𝑉𝑏)
2. La vitesse totale de l’air peut être exprimée comme une combinaison de la vitesse de convection naturelle 𝑉𝑛 et de la vitesse de convection forcée 𝑉𝑓 : 𝑉𝑏=ℎ(𝑉𝑛+𝑉𝑓)
3. Enfin, nous faisons l’hypothèse d’un régime de convection mixte7, donc la vitesse de convection naturelle peut s’exprimer en fonction de la gravité 𝑔 : 𝑉𝑛=𝑢(𝑔)

On a alors : 𝛿=𝑓(𝑉𝑏)=𝑓(ℎ(𝑉𝑛+𝑉𝑓))=𝑓(ℎ(𝑢(𝑔)+𝑉𝑓))=𝑧(𝑔) L’épaisseur de couche limite 𝛿 peut s’exprimer en fonction de la gravité et donc toutes les équations précédentes régissant les échanges gazeux peuvent être calculées en fonction du paramètre de gravité. Avec : 𝑉𝑏, la vitesse de l’air ; 𝑉𝑛, la vitesse de convection naturelle ; 𝑉𝑓, la vitesse de convection forcée ; et 𝑔, la gravité.

3. Résultats et discussion Les résultats présentés ci-dessous ont été obtenus en faisant une simulation avec le modèle précédemment décrit, avec les paramètres détaillés dans le Tableau 1. 3.1. Comment l’épaisseur de couche limite varie-t-elle en fonction de la gravité et de la convection forcée ? Dans cette première partie, nous regardons les variations de l’épaisseur de la couche limite pour différentes valeurs de gravité (entre 0 m.s-2 (impesanteur) et 9.807 m.s-2 (1g, gravite terrestre)) et 5 valeurs de convection forcée. Les résultats sont donnés dans la Figure 2. Plus les valeurs de la gravité et de la convection forcée sont grandes, plus l’épaisseur de la couche limite est faible. En gravite lunaire (1.625 m.s-2) sans convection forcée, la couche limite est 50% plus épaisse qu’en gravité martienne (3.711 m.s-2). A noter qu’en gravité terrestre, la couche limite est 2 fois plus petite avec une ventilation forcée de 1m/s que sans ventilation.

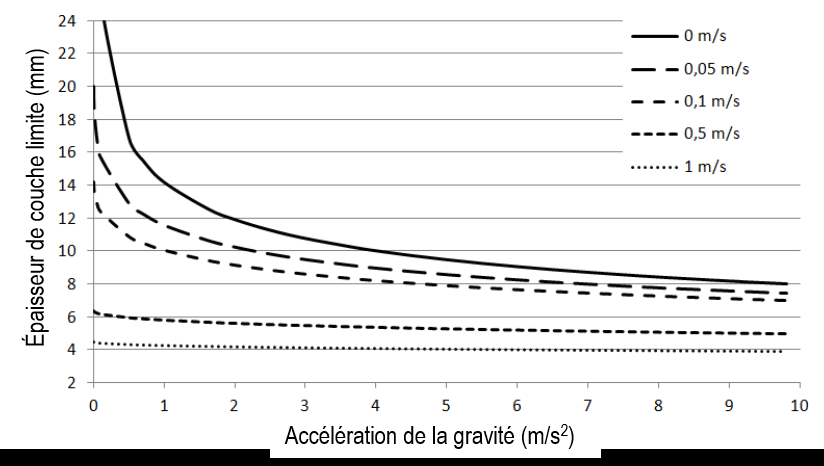
L’épaisseur de couche limite est plus sensible aux variations des niveaux de gravité pour de faibles niveau de ventilation. En effet, en gravité terrestre, la vitesse de convection naturelle calculée à partir du modèle avec les paramètres d’entrée donnés ci-dessus est de 0.3 m.s-1 donc au-delà de cette valeur, la convection forcée prévaut sur la convection naturelle. Cela souligne l’existence d’une valeur limite pour la convection forcée en-dessous de laquelle l’épaisseur de couche limite dépend des niveaux de gravite et au-dessus de laquelle elle dépend principalement de la vitesse de convection forcée. Ce modèle de couche limite est valable pour une seule feuille ronde et sera différent pour une plante entière, puisque la forme de la plante est plus complexe. Pour une canopée8 il faudra prendre en compte l’épaisseur de couche limite de la canopée entière.

3.2. Comment la production de nourriture varie-t-elle en fonction de la gravité et de la convection forcée ? Dans cette deuxième partie, nous avons fait une simulation de la quantité de biomasse produite par une laitue sur une période de 50 jours, pour trois valeurs de gravité (impesanteur, martienne et terrestre) et trois vitesses de convection forcée.

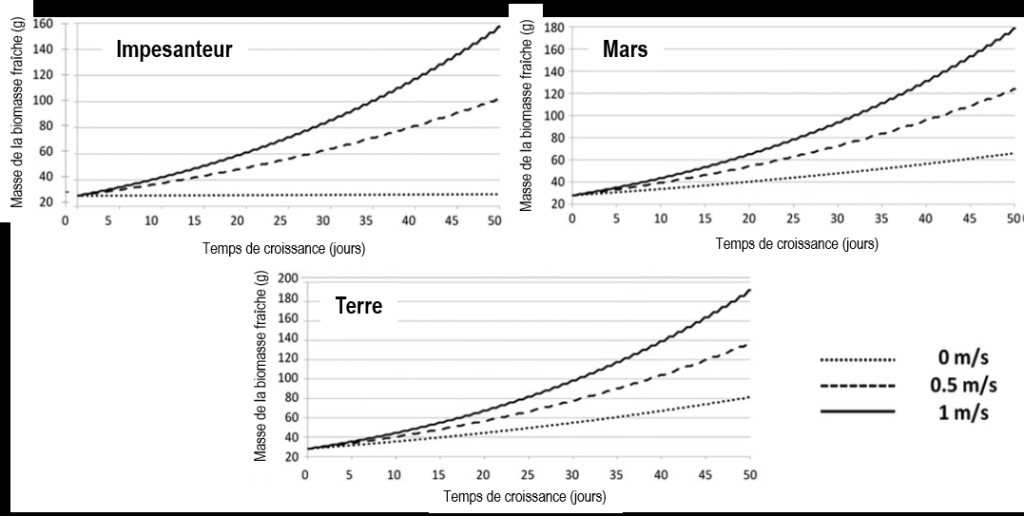
Il est à souligner qu’en gravité terrestre, au bout de 50 jours, la production de biomasse est 2.5 fois plus importante avec une vitesse de convection forcée de 1 m/s que sans convection et 40% plus importante avec 0.5 m.s-1. Sans convection forcée, la production de biomasse est 25% plus importante en gravité terrestre qu’en gravité martienne. Et avec une convection forcée de 0.5 m.s-1, elle est 20% plus importante en gravité martienne qu’en impesanteur. Ceci souligne l’importance d’ajuster la ventilation à un niveau adéquat dans des environnements de gravité réduite, pour obtenir des rendements équivalents aux rendements terrestres. Pour prédire la quantité de nourriture qui pourra être produite lors des missions spatiales longue durée, il sera donc crucial d’étudier les relations complexes entre convection forcée, niveau de gravité et production de biomasse.

4. Conclusion

Cette étude souligne l’importance d’une bonne compréhension des interactions entre la convection et de la gravité sur la couche limite, pour être en mesure de prédire de manière fiable les quantités de biomasse, d’eau et de dioxygène qui pourront être produites. La prochaine étape sera d’ajouter un bilan énergétique à ce bilan de masse et de s’intéresser aux variations de la température de la surface des feuilles en fonction de la gravité et de la convection. Ces résultats seront validés par une expérimentation en vol parabolique et l’objectif final est d’aboutir à un modèle précis de la croissance des plantes en gravité réduite.

Notes :

1. Abrégé LSS pour Life-Support System en anglais
2. Système support-vie micro-écologique alternatif
3. Abrégé ESA pour European Space Agency en anglais
4. La convection naturelle est le résultat de l’ascension des masses d’air moins denses (air chaud) qui provoque un brassage de l’air naturellement sur Terre
5. Lorsqu’un obstacle solide est placé dans un fluide en écoulement (ici l’obstacle est la feuille et le fluide est l’air), une couche de ce fluide se forme à la surface du solide, qui a une vitesse inférieure ou égale à 99% de la vitesse du reste du fluide à l’infini (c’est-à-dire loin de l’obstacle)
6. De l’expérience et de l’observation
7. En convection mixte, les ordres de grandeur de la convection naturelle et de la convection forcée sont égaux
8. Partie supérieure d’un ensemble de plantes

Références Beek, W.J., Muttzall, K.M.K., and van Heuven, J.W. (1999) Transport Phenomena, 2nd ed.Wiley, Chichester andNew York. Hézard, P. (2012) Higher Plant Growth Modelling for Life Support Systems: Global Model Design and Simulation of Mass and Energy Transfers at the Plant Level. PhD thesis, Doctoral School of Life Sciences, Health, Agronomy, Environment. Université Blaise Pascal, Université d’Auvergne, Clermont-Ferrand. Kitaya, Y., Kawai, M., Tsuruyama, J., Takahashi, H., Tani, A., Goto, E., Saito, T., and Kiyota, M. (2003a) The effect of gravity on surface temperatures of plant leaves. Plant Cell Environ 26:497–503. Mitchell, C.A. (1994) Bioregenerative life-support systems. Am J Clin Nutr 60:820S–824S. Wheeler, R.M. (2004) Horticulture for Mars. Acta Hortic 642:201–215.

*****

Retrouvez tous les articles du Journal Décoder ici!