Article original : : « TWINCLE : A Constrained Sequential Rule Mining Algorithm for Event Logs », 21st KES International Conference, 2017 Proposé par : Benjamin Dalmas, Enseignant-Chercheur Institution : Mines Saint-Etienne Laboratoire : Laboratoire d’Informatique, de Modélisation et d’Optimisation des Systèmes
Article relu et amendé par : : la classe de 3^ème du collège Albert Camus de Mme Chaumeil
Adresse : Collège Albert Camus, Rue du Sous-marin Casabianca, 63000 Clermont-Ferrand

*****

Résumé

Lorsque l’on essaye de définir un parcours de soins “standard” à l’hôpital, il faut faire appel à des méthodes qui agrègent chaque parcours de chaque patient en un parcours unique, une sorte de “résumé”. Cet exercice est souvent compliqué à cause de la nature aléatoire des parcours de soins. En matière de santé, il arrive que les choix que l’on a fait dans le passé (ex : prendre des médicaments) impactent les choix que l’on va faire dans le futur (ex : possibilité d’opération). Ces relations se perdent durant l’étape d’agrégation. Nous allons voir qu’il est possible de les retrouver.

Mots-clefs

Parcours de soins / règles d’association / relations / interventions

1. Contexte

Un virage mal négocié en ski, une glissade dans les escaliers ou encore une chute à vélo, on a tous déjà expérimenté les désagréments d’une blessure. Parce qu’un bras cassé ou une entorse à la cheville est si vite arrivé, rares sont ceux qui n’ont jamais mis les pieds à l’hôpital ! Et quand vous vous rendez à l’hôpital, souvent vous y passez beaucoup de temps. Vous attendez des heures aux urgences pour finalement ne voir un médecin que quelques minutes (secondes) ? Vous vous dites “tout ça pour ça”, “ce n’est pas normal d’attendre autant” ou encore “tout ce monde aux urgences…” ?

Et bien nous aussi.

Si on devait trouver les facteurs qui expliquent ce problème, on parlerait du nombre important de patients à l’hôpital ou du manque de personnel médical pour prendre en charge toutes ces personnes. Mais le principal coupable dans tout ça, c’est la santé elle-même. Et oui, lorsqu’on juge le système de santé en général, on regarde souvent ce qui nous arrive seulement à nous. Faire un scanner et un plâtre pour un bras cassé, ça ne semble pas hyper compliqué à gérer après tout, ça devrait filer droit à l’hôpital. Mais si on prend un peu de recul, et que l’on regarde ce qu’il se passe pour toutes les personnes qui ont eu un bras cassé, et bien ce n’est plus du tout la même chose. Alors que vous avez eu juste à faire un scanner et poser un plâtre, d’autres patients ont peut-être eu des complications et ont dû subir d’autres interventions.

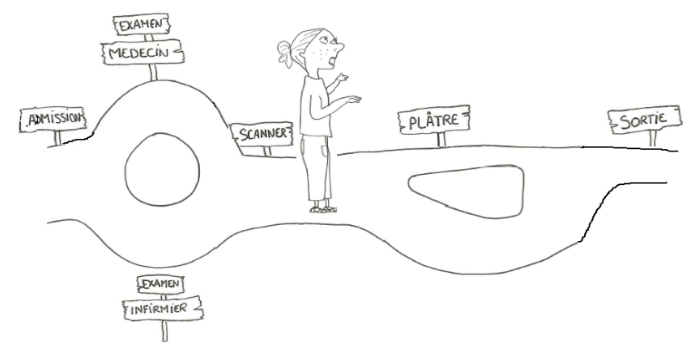
En fait, ça va dépendre de beaucoup de facteurs, tels que votre état de santé, votre situation familiale ou encore vos activités quotidiennes. Et tout cela, c’est spécifique à chaque personne. On remarque donc un phénomène aléatoire dans la prise en charge des patients. Et dans le domaine de la santé, on n’aime pas beaucoup l’aléatoire. L’idée que tout ne se passe pas de la même manière quand il s’agit de soigner des êtres humains, ce n’est pas la meilleure situation pour être efficace.

Pour tout problème de santé (maladie, fracture, …), on va appeler “parcours de soins” l’ensemble des interventions effectuées pour résoudre ce problème. Pour illustrer ce concept, prenons comme exemple trois patients : Pierre Le Bon, Paul La Brute et Jacques Le Truand. Tous les trois sont arrivés aux urgences en même temps pour un bras cassé, mais ont eu des expériences différentes.

Si on regarde le parcours de Pierre Le Bon, il a été admis aux urgences et a vu un médecin. Il a ensuite effectué un scanner pour finalement se faire poser un plâtre. Enfin, il a pu repartir chez lui. On suppose donc que ce parcours de soins est celui suivi par toutes les personnes qui viennent aux urgences pour un bras cassé. Pour vérifier, on va regarder celui des autres patients.

Pour Paul La Brute, le parcours est similaire à celui de Pierre, à l’exception près qu’il n’a pas eu besoin de plâtre car ce n’était pas si grave. Il est donc reparti chez lui juste après le scanner. Enfin, Jacques le Truand a suivi le même parcours que Paul, mais a été examiné par une infirmière et non un médecin.

            On remarque donc que chaque patient a un parcours de soins différent qui lui est propre. Dans cet exemple il n’y a que 3 patients, mais lorsqu’il y en a des milliers, cela devient très compliqué pour les médecins de s’y retrouver et de savoir qui a fait quoi ! Pour simplifier leur compréhension, on va agréger tous les parcours de soins en un seul et créer un “parcours général”, qui représente le parcours de soins suivi par la majorité des patients.

Pour notre exemple du bras cassé, ce parcours ressemble à celui montré dans la Figure 1. On remarque que les trois parcours de soins sont agrégés en un seul, une sorte de “résumé”.  Cette version du parcours de soins pour les patients avec un bras cassé est plus compréhensible pour les médecins que tous les parcours individuels.

Par contre, on peut voir que cette méthode d’agrégation a un inconvénient majeur. Si  on reprend le parcours présenté dans la  Figure 1, il est possible de réaliser les quatre parcours présentés dans le Tableau 1.  Parmi eux, on retrouve bien sûr les parcours individuels de nos trois patients Pierre, Paul et Jacques : ce sont les trois premiers. Mais il est aussi possible de réaliser un autre parcours, comme indiqué par la colonne « Inconnu » dans le Tableau 1.

Mais pourquoi un parcours qui n’a pas été observé chez nos patients apparaît dans le parcours général ? Et bien ce phénomène est un effet de bord de l’agrégation : en voulant généraliser, on perd le détail des parcours individuels. La

raison ? Tout simplement parce que dans le parcours, il y a des choix [van der Aalst, 2016]. Plus particulièrement, il y en a deux :

1. être examiné par un médecin ou une infirmière
2. se faire poser un plâtre ou non

Plus il y a de choix, plus il y aura de chance que le parcours général soit composé de parcours qui n’ont jamais été observés. Et bien qu’un parcours général soit facile à analyser et apporte beaucoup d’information, ces “faux parcours individuels” peuvent induire en erreur, et cela peut être assez problématique lorsque le parcours prend en charge des patients atteints de maladies graves.

• Présentation du problème

Dans cet article, on propose une méthode pour éliminer ces “faux parcours“ qui polluent l’analyse. Pour faire cela, on va utiliser une technique en informatique qui s’appelle : les règles d’association [Agrawal et al., 1993].

Une règle d’association est une méthode populaire dont l’objectif est de découvrir des liens entre les données. Une règle d’association est notée r: X→Y, où X et Y sont des ensembles d’interventions dans notre cas. L’objectif est de savoir si les interventions contenues dans X ont un impact sur les interventions contenues dans Y.

 Pour illustrer ce concept un peu flou, prenons un exemple issu du parcours de soins des patients avec un bras cassé présenté dans le Tableau 1. Dans ce parcours, on peut vouloir savoir si les patients qui ont été examinés par un médecin ont aussi eu un plâtre. Cette règle, elle s’écrit :

r : {exam. médecin}→{plâtre}

On évalue l’importance d’une règle d’association r en mesurant sa “confiance”, notée conf(r). La confiance est égale au nombre de patients qui ont exécuté X et Y (on appelle ça le support de XY, noté sup(XY)), divisé par le nombre de patients qui ont exécuté X avec ou sans Y (on appelle ça le support de X, noté sup(X)), soit : conf(r) = sup(XY)/sup(X)

Dans notre exemple, conf(r) est donc égale au nombre de patients qui ont vu un médecin et eu un plâtre, divisé par le nombre total de patients qui ont vu un médecin. La confiance de la règle est donc égale à conf(r) = 1/2 = 0,5

Plus une confiance tend vers 0, plus la règle est faible. Dans notre cas, cela signifierait que le fait de voir un médecin n’a pas spécialement d’impact sur le fait de poser un plâtre. A l’inverse, plus une règle a une confiance qui tend vers 1, plus la règle est forte et signifie qu’une auscultation par un médecin a de forte chance de se terminer par une pose de plâtre. Il nous suffit juste de définir un seuil de confiance minimum entre 0 et 1 pour indiquer à partir de quand une règle est intéressante pour nous.

Le nombre d’interventions comprises dans X et Y n’est pas limité. Par exemple, on peut définir une règle

r :  {admission + exam. médecin} → {plâtre}.

 C’est grâce aux règles d’association que l’on va pouvoir détecter les “faux parcours”. Comment ? Et bien quelle est la confiance de la règle r : {exam. infirmière}→{plâtre} ? Elle est égale à 0, cela signifie qu’aucun patient a été examiné par une infirmière et s’est ensuite fait poser un plâtre. Ce “parcours” n’est donc a priori pas possible, et cela tombe bien, car c’est notre parcours inconnu ! La technique des règles d’association est donc très utile pour répondre à notre problématique. Bien sûr, tout n’est pas rose et on va se heurter à quelques obstacles.

On se rend vite compte que le nombre de règles que l’on peut créer peut être grand. Dans notre exemple il y a 6 interventions, le nombre de règles possibles est égal à 602. Mais si l’on passe à 10 interventions (soit juste 4 de plus) et bien le nombre de règles possibles passe à 57 002 ! Et si on a 100 interventions, on passe à environ 5,15×10⁴⁷ !

Le nombre augmente donc très vite et même pour un ordinateur puissant, ça devient très long à calculer.

• Méthode de résolution

Notre objectif est donc clair : réduire au maximum le nombre de règles à calculer.

Et pour cela on va utiliser une caractéristique de la mesure de support : sa propriété anti-monotone ! Illustrons cette propriété : si l’on prend deux interventions A et B, alors le support de A, sup(A), (le nombre de patient qui a effectué A) sera forcément supérieur ou égal au support de AB, sup(AB), (le nombre de patients qui ont effectué A et B). Par exemple, sup(exam. médecin) ≥ sup(exam. médecin + plâtre) car 2 ≥ 1.

Rappelez-vous, la confiance d’une règle r: X→Y est égal àconf(r) = sup(XY)/sup(X). Donc si l’on rajoute des interventions dans Y, sup(XY) va diminuer ou rester égal. Par conséquent, conf(r) va aussi diminuer ou rester égale, étant donné que le numérateur (le XY) diminue ou reste égal, et que le dénominateur (le X) reste le même. Toujours sur le même exemple :

• conf(r1 : {admission}→{exam. médecin}) = 2/3 ≈ 0,66.
• conf(r2 : {admission}→(exam. médecin + plâtre}) = 1/3 ≈ 0,33.

On voit donc que conf(r1)≥conf(r2). Si on définissait le seuil de confiance minimum à 0,5, et bien r1 serait considérée “une bonne règle” et r2 serait considéré “mauvaise” car elle a une confiance trop petite.

C’est donc cette propriété anti-monotone qui va nous aider à réduire considérablement le nombre de règle à calculer et ne choisir que les bonnes !

• Protocole expérimental et résultats

Pour vérifier que notre technique marchait bien, on l’a testée dans un vrai hôpital, en prenant le parcours de soins des personnes âgées qui avaient été admises aux urgences pour insuffisance cardiaque. L’objectif était de voir si les interventions qu’ils subissaient aux début de leur prise en charge avaient un impact sur leur retour à l’hôpital plus tard dans l’année. Il fallait donc trouver quelles séquences d’interventions semblaient être synonymes de retour à l’hôpital. Dans cet exemple il y a 16 Interventions, le nombre total de règles possibles est égal à 42 915 650 !

Nous avons exécuté notre algorithme dans lequel nous avons utilisé les mesures de support et de confiance (et leur propriété anti-monotone) pour éliminer les règles inutiles, mais aussi d’autres mesures comme le temps écoulé entre deux interventions, ou le coût de chaque intervention. Mais nous ne nous attarderons pas sur ces détails ici.

Les résultats ont été très positifs ! Nous avons calculé seulement 21 521 règles, ce qui signifie que notre algorithme a éliminé plus de 99,9% des règles !

• Conclusion

On a présenté dans la première partie le contexte des parcours de soins ainsi que les raisons pour lesquelles il était utile d’avoir un parcours “général” qui représente la majorité des patients. On a ensuite montré que ce parcours comprenait souvent des “erreurs” dues à l’agrégation des parcours individuels et on a présenté l’idée d’utiliser les règles d’association pour résoudre ce problème. Comme le nombre de règles d’association possible devient rapidement très grand et très longues à calculer, la partie suivant a introduit une méthode qui accélère le calcul en réduisant le nombre de règle. Enfin, dans la dernière partie on a montré que cette technique améliorée a été testée sur une application réelle dans un hôpital et que les résultats ont été très satisfaisant.

Bien sûr, il existe d’autres problèmes avec les règles d’association que nous n’avons pas résolus. Par exemple, nous avons calculé l’impact de voir un médecin sur la pose d’un plâtre. Mais il serait aussi intéressant de calculer l’impact de voir un médecin sur la non pose d’un plâtre. Cette différence qui peut sembler infime, voire simple à mesurer, et en fait un problème très complexe. Cela fera peut-être partie de nos recherches futures !

Références

[Agrawal et al., 1993] : Agrawal, R., Imielinski, T., and Swami, A. (1993). Mining association rules between sets of items in large databases. Proceedings of the 1993 ACM SIGMOD International Conference on Management of Data, pages 207–216.

[van der Aalst, 2016] : van der Aalst, W. (2016). Process Mining : Data Science in Action.Springer Berlin Heidelberg.

Comment citer cet article : Benjamin Dalmas et la classe de 3^ème du
collège Albert Camus (Clermont-Fd (Fr)),
Un algorithme pour détecter les choix passés qui impactent les choix futurs, Journal DECODER, 2019

*****

Vous pouvez retrouver tous nos articles ici !