L'auteur de mots croisés
Publié par Atelier Rlv, le 2 février 2022 6.9k
Aujourd'hui nous allons essayer de fabriquer des grilles de mots croisés, mais de façon automatique !
Un jeu de mots
La première grille de mots croisés a été conçue à la main par le journaliste Arthur Wynne et publiée le 21 décembre 1913 dans le supplément du New York World, le Fun. Le jeu s'est beaucoup popularisé en 1924 avec la publication du premier recueil de grilles, alors intitulé « Odd-looking book with pencil attached » (livre à l'allure étrange, avec un crayon attaché). Cette même année, les premiers journaux français et britanniques publient leurs premières grilles.

À la pause, dans le métro, le bus ou la salle d'attente, le cruciverbiste (de cruci « croix » et verbi, « mot ») tente de résoudre une grille en retrouvant les mots qui la composent à l'aide de définitions énigmatiques. Les mots s'imbriquent les uns dans les autres, ce qui apporte encore d'autres indices.
Un problème complexe
Le verbicruciste est celui qui crée la grille. Sa tâche se divise en trois étapes :
- Dessiner la grille : placer les cases noires et identifier les créneaux dans lesquels il va falloir placer les mots.
- Remplir la grille : choisir un mot pour chaque créneau, en faisant bien attention à ce qu'ils se croisent sur des lettres communes !
- Proposer des définitions pour chacun des mots choisis.
La première étape est très facile, on peut même directement utiliser des types de grilles prédéfinis.

La troisième étape n'est pas une mince affaire si on s'y attèle seul. Une grille contient en général une cinquantaine de mots. Si l'on souhaite publier une nouvelle grille par jour sans trop se répéter, il va falloir quelques milliers de mots, et donc quelques milliers de définitions. De plus, une grosse partie du jeu se situe dans la compréhension de ces définitions, qui doivent donc être énigmatiques mais précises. Cacher un terme dans une définition du dictionnaire ne saurait suffire.
Heureusement, il y a une solution : piocher dans ce qui existe déjà. On peut acheter une base de données, ou utiliser de petits outils informatiques pour extraire les définitions depuis des sites de mots croisés en ligne. Cette étape présente donc une difficulté logistique, pas vraiment théorique.
Pour la seconde, en revanche, c'est tout l'inverse. Étant donné une grille et une liste de mots, la remplir semble « simple » : tester toutes les combinaisons de mots, jusqu'à ce qu'on tombe sur une grille légale, où tous les créneaux se croisent bien sur des lettres communes. Mais quiconque s'y essaye constate rapidemment que la tâche est longue (compter entre 8 et 10 heures pour un humain expérimenté) !
La tâche est simple à exprimer mais nécessite de faire beaucoup d'opérations. C'est ce qu'on appelle, en algorithmie, la complexité. Pour avoir un ordre d'idée, on va essayer de remplir une grille classique, avec 50 créneaux. Nous utiliserons un petit dictionnaire, avec seulement 1000 mots. Pour le premier créneau, on a le choix parmi 1000 possibilités. Pour le second, c'est la même chose. On se retrouve déjà à 1000 × 1000 = un million de possibilités (pour simplifier, on ne tient pas compte de la taille des mots ou du nombre de croisements). Avec trois créneaux, on se retrouve à un milliard de possibilités… Avec 50 créneaux, on se retrouve à 10150 possibilités. Il s'agit d'un 1 avec 150 zéros derrière. La complexité est combinatoire, ça explose rapidemment. Nous avons d'ailleurs déjà abordé ce sujet dans une émission : Fil d'étincelles n°1 - À l'assaut des sommets.
Dans la pratique, les humains utilisent beaucoup d'astuces et de raccourcis pour rendre ce problème réalisable. Mais cela reste toujours très long. Pour qu'un ordinateur le fasse à notre place, il faut trouver des astuces similaires mais adaptées à ces cerveaux mécaniques.
La recherche à la rescousse
Pour parvenir à nos fins, nous allons donc devoir ruser. Heureusement, nous ne sommes pas les premières personnes à se poser la question. D'autres ont déjà réfléchi au problème, le tout est de retrouver leurs conclusions.
Comme souvent dans ce cas, on commence par une petite recherche sur Google Scholar. Dans les premiers résultats, il y a une thèse utilisant l'intelligence artificielle pour générer des grilles. Sans l'avoir lu, il est probable que le système qui y est décrit soit trop complexe pour notre petit défi du jour. Mais ces écrits comportent toujours une section dressant un état de l'art. Les thèses sont mêmes de très bonnes ressources pour cela, leurs auteur(e)s sont relativement novices et doivent s'imprégner du sujet dans sa globalité. Ici, ça ne manque pas. Dès le début, un article très intéressant est cité : « A prototype crossword compiler » écrit par P. D. Smith et S. Y. Steen et publié dans The Computer Journal.

Le papier date de 1980, et à l'époque sortait l'IBM PC, qui possède 1000 fois moins de RAM et dont le processeur est 1000 fois plus lent qu'un ordinateur actuel. On ne devrait pas avoir de problème à faire tourner ce programme ! Mais avant cela, il faut le recréer. L'article ne fournit pas de code, mais décrit qualitativement l'algorithme qu'il faut utiliser. Reste donc à en comprendre le fonctionnement.
La méthode : remplir les créneaux un par un à l'aide d'une liste de mots
La méthode est vraiment bête et méchante : tenter de remplir la grille en entier, et revenir en arrière lorsque ça coince. Mais pour la concrétiser, il va falloir préciser un peu plus.
On commence avec une grille vide. Les blocs noirs ont déja été posés.

On identifie tous les créneaux qu'il va falloir remplir. Un créneau correspond à un mot, horizontal ou vertical.
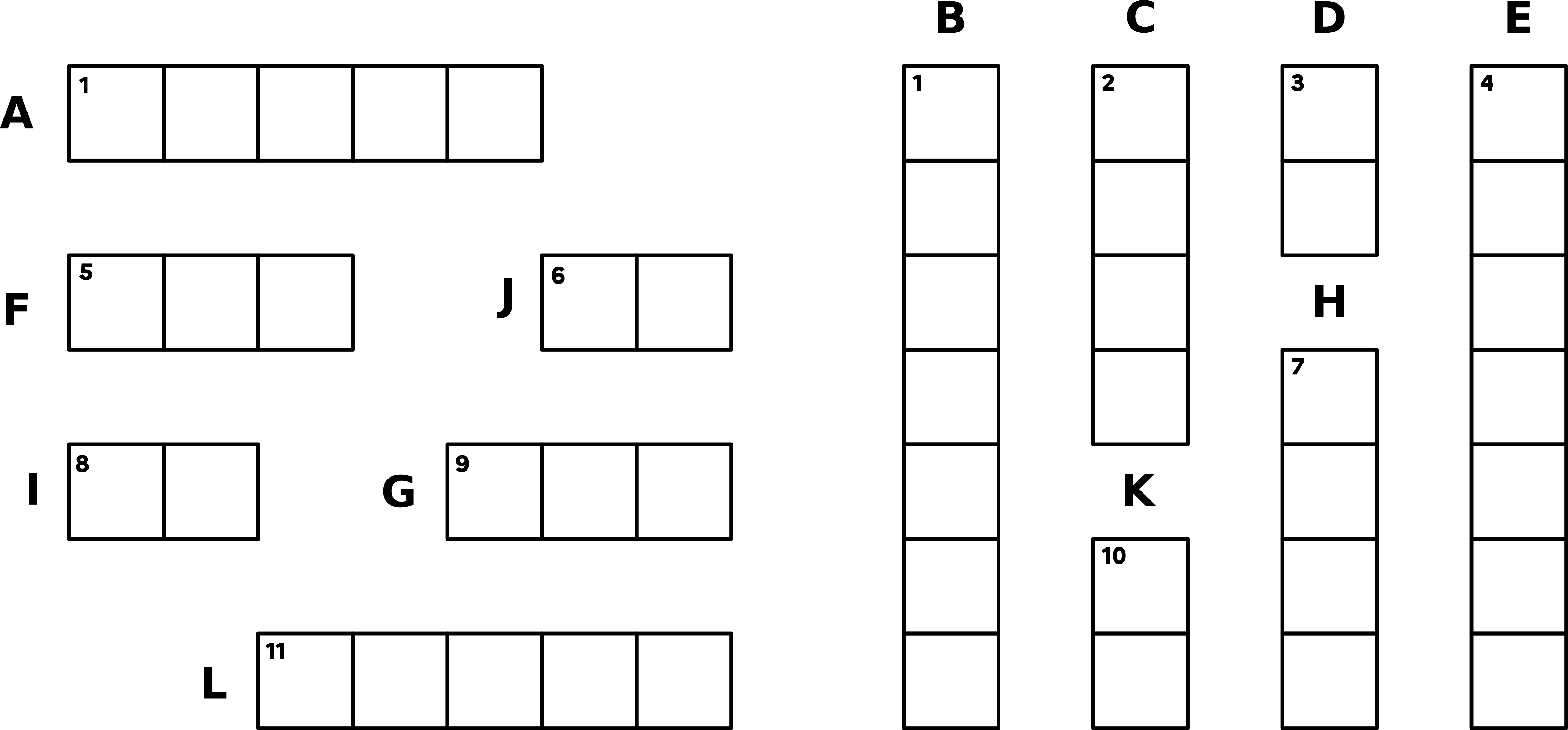
Chaque créneau sera identifié par une lettre (A, B, …, L). Il y en a 12, 6 horizontaux et 6 verticaux.
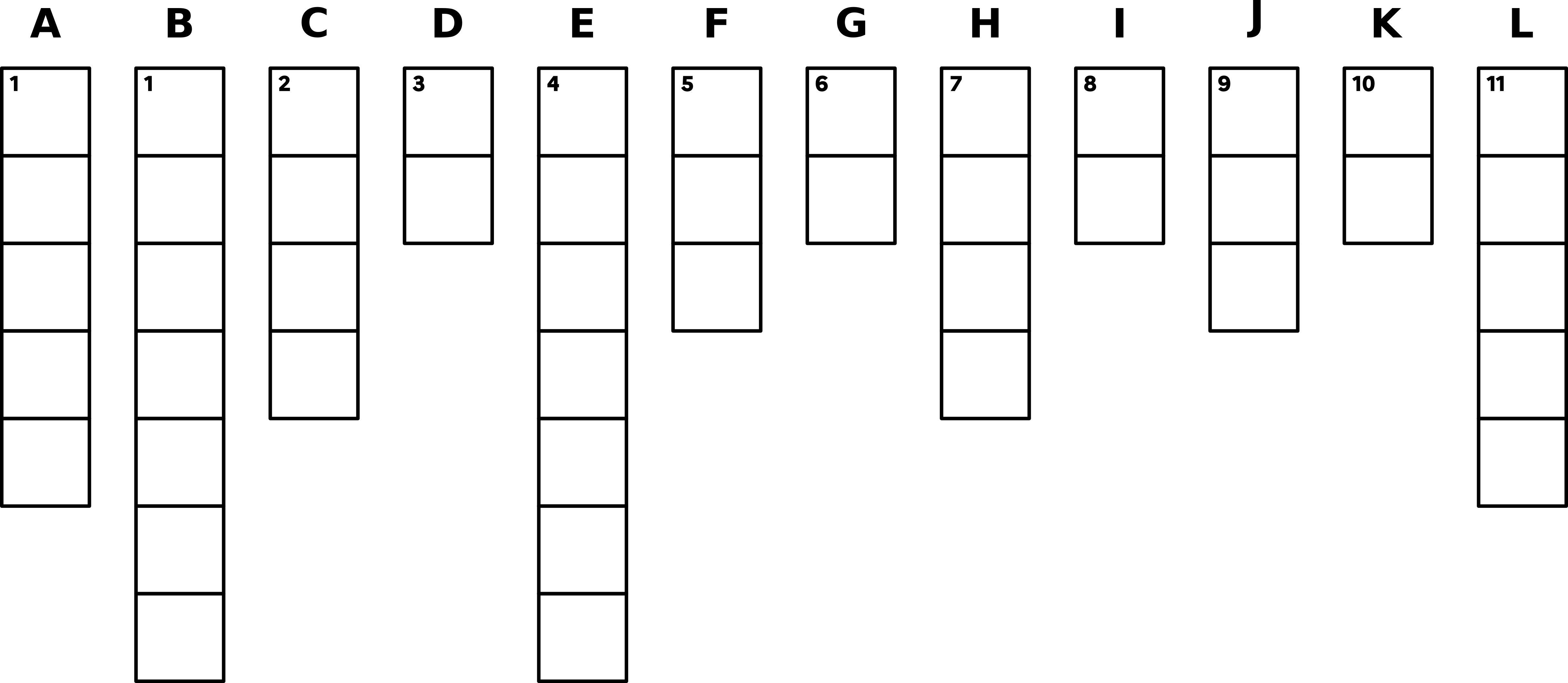
Remplir la grille consiste à trouver un mot pour chaque créneau, en
faisant en sorte que les créneaux se croisent sur une même lettre. Par
exemple, si on choisit TIEDE pour le créneau A, alors il faudra que le créneau B commence par un T, que le créneau C commence par un E et que le créneau D commence par un E.
La recette est donc la suivante :
- Choisir un créneau vide (auquel on n'a attribué aucun mot)
- Faire la liste des mots qui peuvent y rentrer. Au tout début, il n'y aura aucune contrainte (une certaine lettre à une certaine position). Mais plus il y aura de créneaux remplis, plus il y aura de contraintes.
-
Choisir un de ces mots, et l'attribuer au créneau désigné à l'étape 1. Ensuite,
- s'il reste des créneaux à remplir, on repart à l'étape 1,
- mais si tous les créneaux sont remplis, la grille est prête !
- Si tous les mots ont été essayés et qu'aucun ne convient, c'est qu'un des mots précédents est trop contraignant pour la suite. On annule ce qu'on était en train de faire, on revient au créneau précédent, et on essaye de changer de mot.
Prenons un exemple. Admettons que tous les créneaux soient déjà rempli, sauf C et F :

On commence à l'étape 1, on choisit un créneau vide, par exemple C.
Déjà, nous avons une petite contrainte : le mot doit commencer par un E. On fait donc la liste des mots que l'on connaît qui commencent ainsi :
ELAN
ELLE
ERIC
...
Super, la liste n'est pas vide ! On essaye de mettre le premier mot, ELAN.
Comme la grille n'est pas complète, on retourne à l'étape 1, choisir un
créneau vide. Il n'en reste qu'un seul, le F. Deux contraintes se
présentent : le mot doit commencer par Q et finir par A…
Eh bien, quand on fait la liste, on ne trouve aucun mot… Nous sommes
dans le cas de l'étape 4. Il faut annuler notre dernière action (choisir
le mot ELAN pour le créneau C), car elle était trop contraignante. On recommence alors, en choisissant le mot suivant dans la liste : ELLE. Même problème : il faut trouver un mot de trois lettres commençant par Q et finissant par L. Il faut encore recommencer. On essaye alors le mot ERIC. Et là, bingo ! On peut écrire QUI dans le créneau F. La grille est enfin complète.

Tout est une question d'ordre
Malheureusement, nous ne sommes pas encore tirés d'affaires. Si on fabrique un programme qui applique naïvement cette recette, il risque de mettre (très) longtemps. À qui la faute ? L'étape qui consomme le plus de temps, c'est la numéro 2 : lister les mots possibles. Car pour cela, il faut tester chacun des mots connus, et filtrer ceux correspondant aux contraintes de la grille. Il existe des techniques assez subtiles pour efficacement filtrer ces mots, mais quoi que l'on fasse, cette étape restera la plus gourmande en ressources. Il faut donc s'arranger pour avoir à la faire le moins souvent possible.
Chaque fois que l'on tente d'attribuer un mot à un créneau, il faut refaire une liste pour le créneau suivant. Si l'on souhaite faire le moins de listes possible, il faut réussir à remplir tous les créneaux sans trop avoir à revenir sur nos pas.
Les auteurs de l'article proposent justement une telle solution. Il s'agit là de la contribution majeure de l'article, car on passe alors d'un algorithme inutilisable à un algorithme qui fonctionne plutôt bien.
Cette solution repose sur l'ordre de remplissage des créneaux. Précédemment, nous n'avions pas vraiment soulevé ce détail, nous prenions les créneaux dans un ordre aléatoire. Mais si on essaye de fabriquer quelques grilles à la main, on peut vite développer une petite intuition : il vaut mieux commencer par les créneaux « obligatoires » (ceux où il n'y a pas beaucoup de choix), et finir par ceux où beaucoup de choix sont possibles. Cela semble logique, et ce n'est pas pour rien.
Pour illustrer cela, concentrons-nous sur une version plus simple de notre problème :
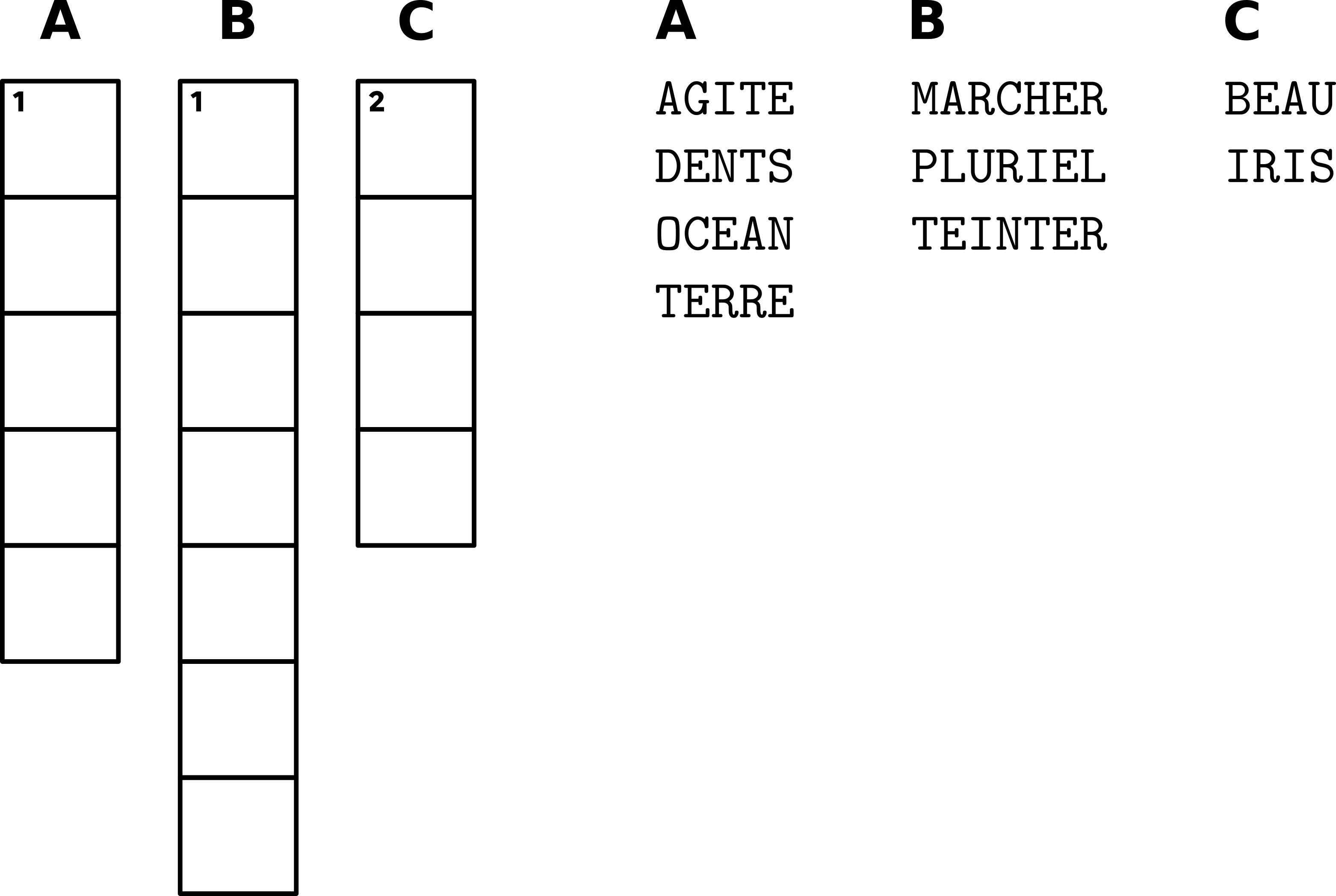
Les créneaux sont les mêmes que dans notre grille d'exemple. En termes de contraintes, cela veut dire que A et B doivent commencer par la même lettre, et C doit commencer par la troisième lettre de B.
Dans un premier cas, on va remplir d'abord A, puis B, et enfin C. Voici ce que ça donne :

Il y a 4 choix pour le créneau A, puis 3 pour le créneau B, et 2 pour le créneau C. Tous les choix peuvent être représentés sous la forme d'un « arbre ». L'appellation vient du point « racine », tout en haut, et des « branches » qui marquent chaque subdivision. Tout en bas, il y a les « feuilles ».
Lorsque l'on essaye de remplir la grille, cela revient symboliquement
à se promener dans l'arbre. On part toujours de la racine, lorsque la
grille est vide. Le premier niveau correspond au créneau A. Quatre
choix/branches s'offrent à nous. On commence par la première, AGITE,
et on poursuit notre descente dans l'arbre. Chaque niveau représente un
mot choisi pour un créneau. Lorsque l'on arrive sur une feuille, toute
la grille est remplie. Par exemple, la première feuille (tout à gauche),
correspond au mot AGITE pour A, MARCHER pour B et BEAU pour C.
Durant cette promenade (en termes techniques, on parle plutôt d'exploration), on passe de niveau en niveau en suivant des traits. Chaque trait correspond donc à « une étape 3 ». Dans l'exemple ci-dessus, on compte 40 traits.
Maintenant, changeons l'ordre de remplissage des créneaux. On commence par C (2 choix possibles), puis B (3 choix possibles) et enfin A (4 choix possibles).

Il y a exactement le même nombre de feuilles (24), donc le même nombre de remplissages différents de la grille. C'est normal, toutes les possibilités sont représentées. Par contre, on ne compte plus que 32 traits ! En commençant par les créneaux avec le moins de choix, on arrive plus vite aux feuilles.
Avec une grille plus large, la différence est vite significative ! Choisir l'ordre de remplissage des créneaux en amont et intelligemment permet de passer d'un temps moyen de génération de plusieurs heures ou jours à seulement quelques secondes.
Une démonstration ?
Si vous souhaitez voir ce que donne cet algorithme en pratique, en voici une implémentation : https://ychalier.github.io/rlv/crosswords.
Il est possible de régler la taille et la disposition de la grille. Voici par exemple :
Pour voir le code source (la traduction en code de tous les mécanismes décrits dans cet article vous pouvez consulter le dépôt GitHub.
Les définitions utilisées proviennent du site de Ouest-France, qui propose des mots-fléchés en ligne.
Un petit bonus statistique
La méthode présentée dans cet article utilise la génération mot-à-mot. Mais certaines méthodes essayent plutôt de remplir la grille lettre par lettre. Ces méthodes s'adapteny mieux aux grilles où beaucoup de créneaux sont imbriqués, mais nécessitent de constamment vérifier que les mots qui sont écrits existent bel et bien.
Pour faire cela, ces méthodes reposent beaucoup sur la « distribution » des lettres au sein des mots, c'est à dire, en quelques sortes, leur position préférée, la plus fréquente.
En prenant les mots du site de démonstration, on obtient ces résultats :
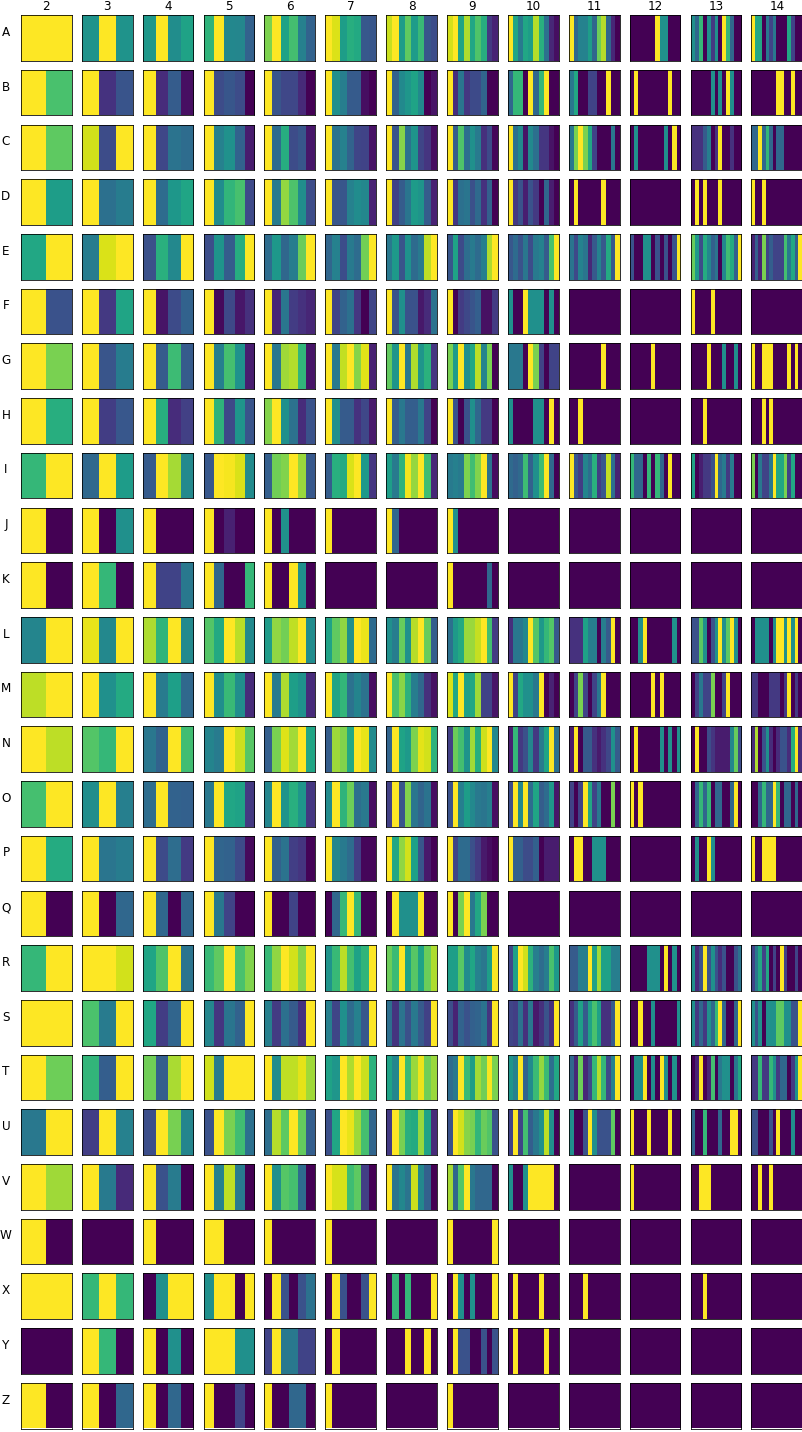
S apparaît surtout à la fin des mots, et le O surtout en deuxième position.
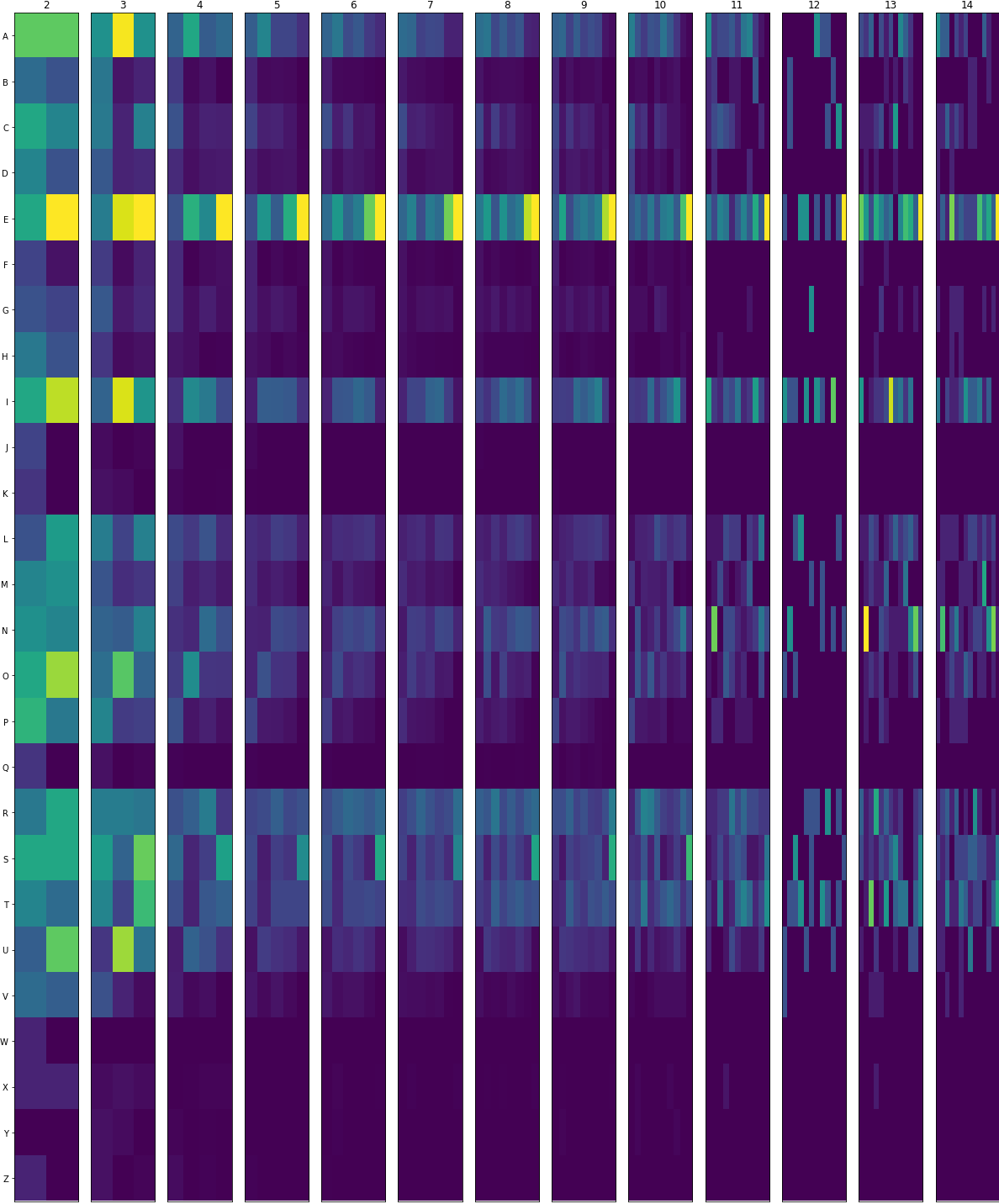
A, un C ou un E.




